CÂN BẰNG ĐỘNG MỘT MẶT PHẲNG – PHƯƠNG PHÁP VECTOR

CÂN BẰNG ĐỘNG MỘT MẶT PHẲNG – PHƯƠNG PHÁP VECTOR

CÂN BẰNG ĐỘNG MỘT MẶT PHẲNG – PHƯƠNG PHÁP VECTOR, là phương pháp đơn giản và dễ thực hiện. Hiện tượng mất cân bằng động (Unbalance hay Imbalance) thường được định nghĩa là việc phân phối không đồng đều khối lượng của rotoa quanh trục quay của nó. Hay đơn giản hơn là trọng tâm của vật quay không nằm trên tâm quay. Vật quay có thể được cân bằng tại chỗ hoặc trong máy cân bằng động khi mà chúng ta giả sử mất cân bằng động là vấn đề và khối lượng (đối trọng) có thể được thêm vào hoặc lấy bớt đi để mà kéo trọng tâm vật quay về tâm quay. Các máy cân bằng động hiện nay đều có thể tính toán thuật toán này và sẽ chỉ ra khối lượng và vị trí cần thêm vào. Một số máy mới hơn chẳng hạn như SMC có chức năng như khuyến cáo khối lượng cục thử, chia cục thử hoặc tính lượng lấy ra.  Tuy nhiên, cách cổ điển là vẽ biểu đồ cực với các vector bằng cách đo đạc kết hợp giữa máy phân tích và đèn chớp (đo tốc độ, góc pha).

Định nghĩa.

• Vector – là một đại lượng có phương và biên độ.
• Polar Graph Paper – giấy biểu đồ với các vòng tròn đồng tâm cách đều nhau chia thành các vòng cung nhỏ.
• Microns – độ rung chuyển vị từ đỉnh đến đỉnh. Thường được sử dụng trong cân bằng trường.
• Trial Weight – khối lượng được thêm vào vật quay nhằm làm thay đổi điều kiện mất cân bằng.
• O – Vector đại diện cho sự mất cân bằng ban đầu.
• O + T – Vector đại diện cho sự mất cân bằng sau khi thêm khối lượng thử.
• T – Vector đại diện cho sự khác biệt giữa  “O” và (“O”+”T”). Đây chính là hiệu ứng của khối lượng thử.
• A – góc giữa “O” and “T”

Giải bài toán CÂN BẰNG ĐỘNG MỘT MẶT PHẲNG – PHƯƠNG PHÁP VECTOR.

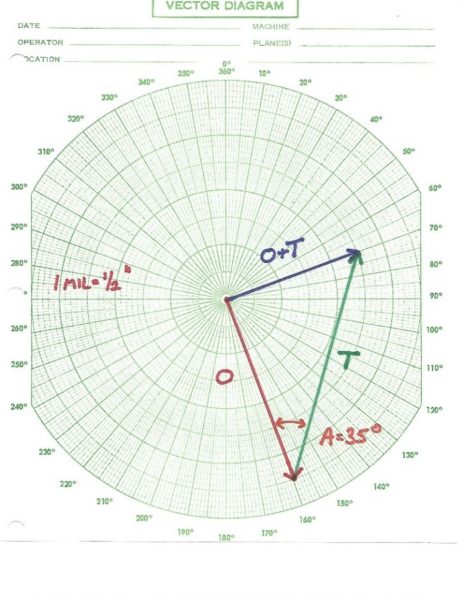
1. Ở tốc độ vận hành, ta đo biên độ rung chuyển vị và pha ở 1 x vòng / phút. Sau đó vẽ Vector O. Theo hình vẽ bên “O” = 7 mils tại góc 160 độ.
2.  Tắt máy và thêm cục khối lượng thử với một khối lượng nhất định. Vd: Khối lượng thử = 100 grams (3.53 oz).
3. Chạy máy và thu thập dữ liệu: biên độ mới và pha mới. Vector mới này được vẽ lên biểu đồ ký hiệu là  “O” + “T”. Theo hình bên: “O” + “T” = 5 mils tại 70 độ.
4. Vẽ một Vector từ đầu Vector “O” đến đầu vector “O” + “T” và đặt tên là “T”. Đây thực chất là phép trừ vector mà chúng ta học năm lớp 10 ở Trung học.
5. Đo độ lớn (chiều dài) “T”. Theo hình bên “T” = 9 mils.
6. Sử dụng công thức sau: Khối lượng đúng cần thêm vào = Khối lượng thử x “O”/”T”. Theo hình trên CW = 100 x 7/9 = 77.77 grams.
7. Đo góc giữa “O” và “T” với một thước đo góc. “A” = 35 độ.
8. Mục đích là điều chỉnh vector “T” để nó bằng và đối diện với vector “O”
9. Tháo trọng lượng thử và thêm trọng lượng hiệu chỉnh 77,77 gram 35 độ từ vị trí của trọng lượng thử.
10. Trong ví dụ này, trọng lượng hiệu chỉnh được dịch chuyển theo hướng ngược lại với sự dịch chuyển từ “O” đến “O” + “T”.

Như vậy là chúng ta đã có thể cân bằng động với máy phân tích và đèn nháy rồi đấy. Chúc các bạn thành công.

– nguồn tham khảo: “A Vector Approach to Single Plane Balancing” by Michael Keohane, Vibralign – 

– Người dịch Trần Duy Hoài + Google dịch –